Введение в экспертные системы
Законченное пространство поиска...
Законченное пространство поиска в головоломке "миссионеры и каннибалы ", сформированное алгоритмом поиска в глубину
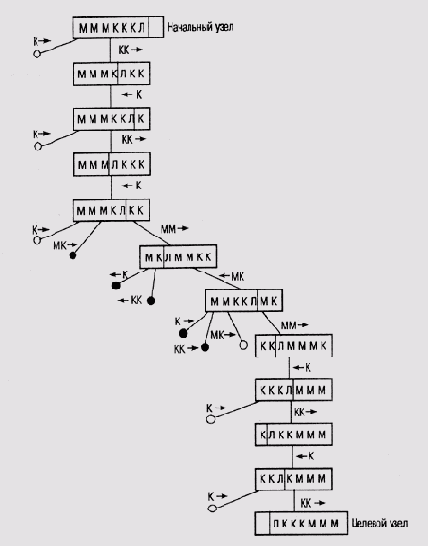
В процессе поиска было развернуто 22 узла, а путь, приводящий к успеху, содержит 11 узлов. Таким образом, оценка проницательности поиска равна 11/22=0.5. Грубо говоря, проницательность поиска говорит нам о том, насколько данный алгоритм позволил избежать выполнения ненужной работы в процессе Поиска решения. Чем выше значение проницательности поиска для того или иного алгоритма, тем лучше.
I) Выберите представление состояний на берегах реки и разработайте программу, которая решает эту задачу, используя оба варианта алгоритмов поиска— в глубину и в ширину. С разными способами формализации этой
задачи можно познакомиться в работе Амарела [Amarel, 1968]. Обратите внимание на то, что существуют способы представления состояний, которые позволяют более экономно использовать вычислительные ресурсы при решении задачи.
II) Попытайтесь улучшить оценку проницательности поиска, полученную для алгоритма поиска в глубину (рис. 2.8), изменив порядок, в котором анализируются в каждом очередном состоянии дозволенные операторы.
III) Обобщите программу как в части количества пассажиров в лодке, так и в части количества миссионеров/каннибалов. Сделайте их параметрами программы, задаваемыми извне. Если вы начнете проводить эксперименты с такой программой, то убедитесь, что, во-первых, эти параметры нельзя варьировать независимо, поскольку при некоторых комбинациях задача не имеет решения, а во-вторых, увеличение значений любого из параметров существенно расширяет пространство поиска.
7. Другая классическая головоломка, знакомая в несколько ином виде многим еще со школьной скамьи, — "Восьмерка". В головоломке принимает участие восемь пронумерованных фишек, которые могут перемещаться по игровому полю 3x3. Цель состоит в том, чтобы из некоторого случайного расположения фишек перейти к упорядоченному (рис. 2.9).
Мы несколько модифицируем ограничения, сформулировав их в терминах перемещения единственного "пустого поля".